My Ph.D. project amis to analyze the data collected by the Belle II experiment, where collisions of electrons and positrons primarily result in the production of \(B \bar B\) pairs. These \(B\) mesons quickly decay into other particles through various decay chains. The final-state particles leave their signatures (trajectories & clusters) in detectors. By analyzing these observations, I reconstruct the physics processes and extract quantities of interest.
Physics analysis
The Standard Model (SM) of particle physics successfully describes most phenomena oberved in collider experiments. Precise measurments of its model parameters and searches for fingerprints beyond the SM are crucial to enhence our understanding of fundamental building blocks of matter and how they interact with each others.
By reconstructing \(\boldsymbol{\bar B^0 \to D^{*+}\ell^-\bar\nu_\ell}\) decays (with \(\ell=e, \mu\)) from a dataset that has about \(2\times 10^8\) \(B \bar B\) pairs, I measured its partial decay rates in bins of kinematic variables. The values of the CKM matrix element \(⎮V_{cb}⎮\) and form factor parameters are determined to simultaneously describe the observed partial decay rates best.
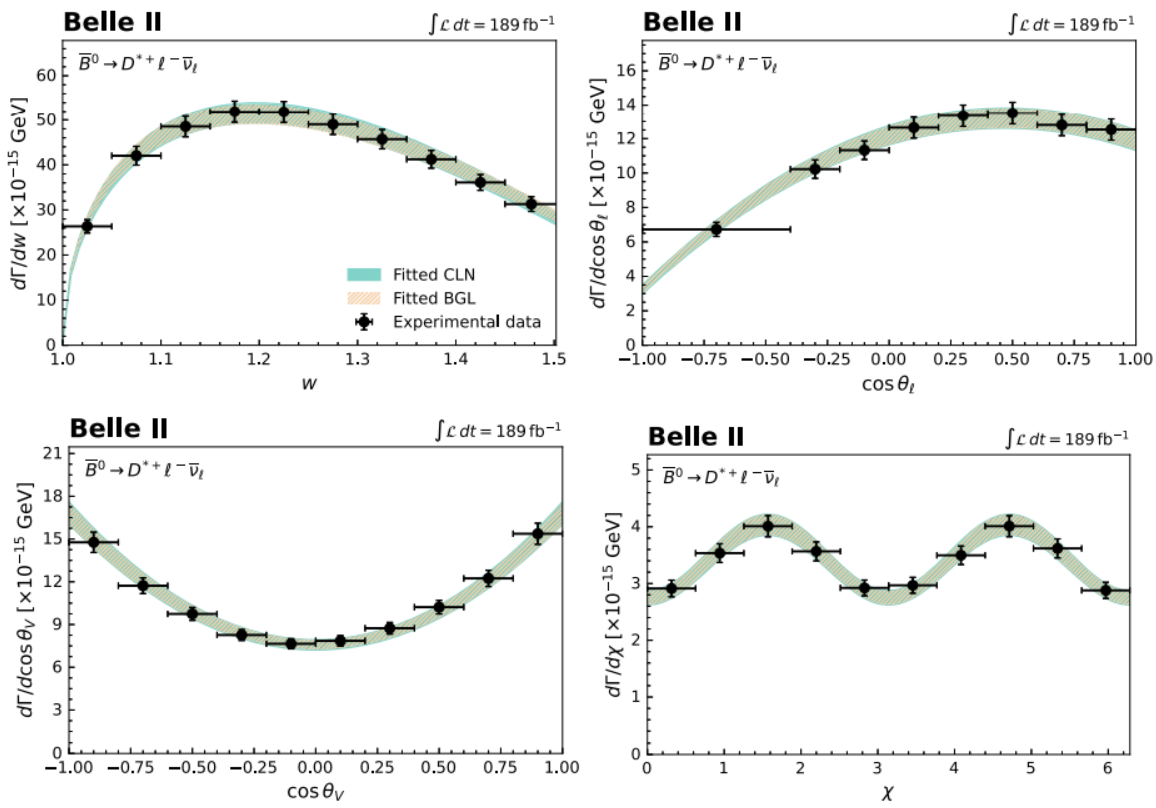
I find
\[|V_{cb}|_\text{BGL}=(40.57\pm 0.31\pm 0.95 \pm 0.58)\times 10^{-3}, \\ |V_{cb}|_\text{CLN}=(40.13\pm 0.27\pm 0.93 \pm 0.58)\times 10^{-3},\]for the Boyd-Grinstein-Lebed and Caprini-Lellouch-Neubert parametrizations respectively, where the uncertainties denote statistical components, systematic components, and components from the lattice QCD input, respectively. The precision is limited by the slow pion tracking efficiency.
In addition, the lepton flavor universality tests are carried out by examining the ratio of branching fractions \(R_{e/\mu}\), and differences of lepton angular asymmetry \({\cal A}_{FB}\) and longitudinal \(D^{*+}\) polarization fractions \(F_L\) between the \(\bar B^0 \to D^{*+}e^-\bar\nu_e\) and \(\bar B^0 \to D^{*+}\mu^-\bar\nu_\mu\) decays. The results are summarized in the table below. All observations are compatible with the SM predictions.
| Decay | Branching fraction | \({\cal A}_{FB}\) | \(F_L\) |
|---|---|---|---|
| \(e\) mode | \((4.917\pm 0.032\pm 0.216)\%\) | \(0.228\pm 0.012 \pm 0.018\) | \(0.520\pm 0.005 \pm 0.005\) |
| \(\mu\) mode | \((4.926\pm 0.032\pm 0.231)\%\) | \(0.211\pm 0.011 \pm 0.021\) | \(0.527\pm 0.005 \pm 0.005\) |
| \(R_{e/\mu}\) | \(0.998\pm 0.009\pm 0.020\) | - | - |
| Difference | - | \((-17\pm 16\pm 16)\times 10^{-3}\) | \(0.006\pm 0.007\pm 0.005\) |
More details can be found in Phys.Rev.D 108 (2023) 9, 092013.
Calibration of particle identification
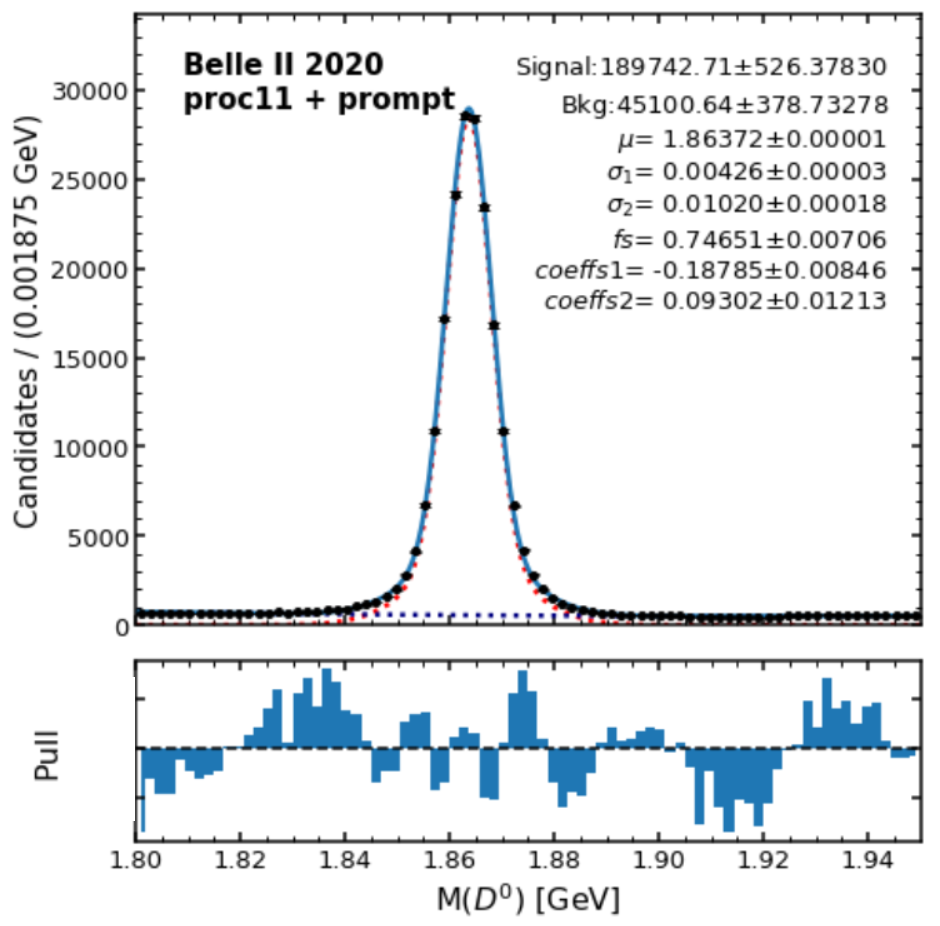
Monte Carlo (MC) samples are generated to study the experimental data. However, they may have different particle identification efficiency. To address this problem, I reconstructed the \(D^*{^+}\to D^0(\to K^-\pi^+)\pi^+\) decay. The signal events (\(D^0\) mesons are correctly reconstructed) are described by two Gaussians with a common mean in the \(m_{D^0}\) distribution, and backgrounds are modeled by Chebyshev polynomials of the second order.
The identification efficiencies for kaons and pions are estimated at various particle likelihood ratios in bins of the polar angle and momentum. The ratios of efficiencies between MC samples and experimental data are used as correction factors.
Calibration of slow pion tracking efficiency
Slow pion tracking efficiency plays a crucial role in semileptonic measurements, as it is the leading order systematic uncertainty for the \(\bar B^0 \to D^{*+}\ell^-\bar\nu_\ell\) decays. Additionally it also impacts the analyses of the \(\bar B^0 \to D^{*+}\tau^-\bar\nu_\tau\) decay.
The tracking efficiency is calibrated by reconstructing the \(B^0\to D^{*+}(\to D^0\pi^+)\pi^-\) decay. The determination of signal events rely on the binned probabilty density function provided by the simulated samples. The tracking efficiency in the low momentum region is calculated relative to the high momentum region.